Classwork Questions
This classwork covers limits from sections 1.1 to 1.4. Solve each problem and then click the button to check your solution!
Question 1: Find the limit by factoring.
\[ \lim_{x \to 3} \frac{x^2 - 9}{x - 3} \]
\[ \lim_{x \to 3} \frac{(x - 3)(x + 3)}{x - 3} = \lim_{x \to 3} (x + 3) = 6 \]
Question 2: Find the limit at infinity.
\[ \lim_{x \to \infty} \frac{2x^3 - 5x + 1}{4x^3 + 7x^2} \]
Limit is ratio of leading coefficients: \[ \frac{2}{4} = \frac{1}{2} \]
Question 3: Find the limit of the trigonometric function.
\[ \lim_{x \to 0} \frac{\sin(4x)}{x} = 4 \]
\[ \lim_{x \to 0} \frac{4 \sin(4x)}{4x} = 4 \]
Question 4: Find the limit from the graph. Does the limit exist?
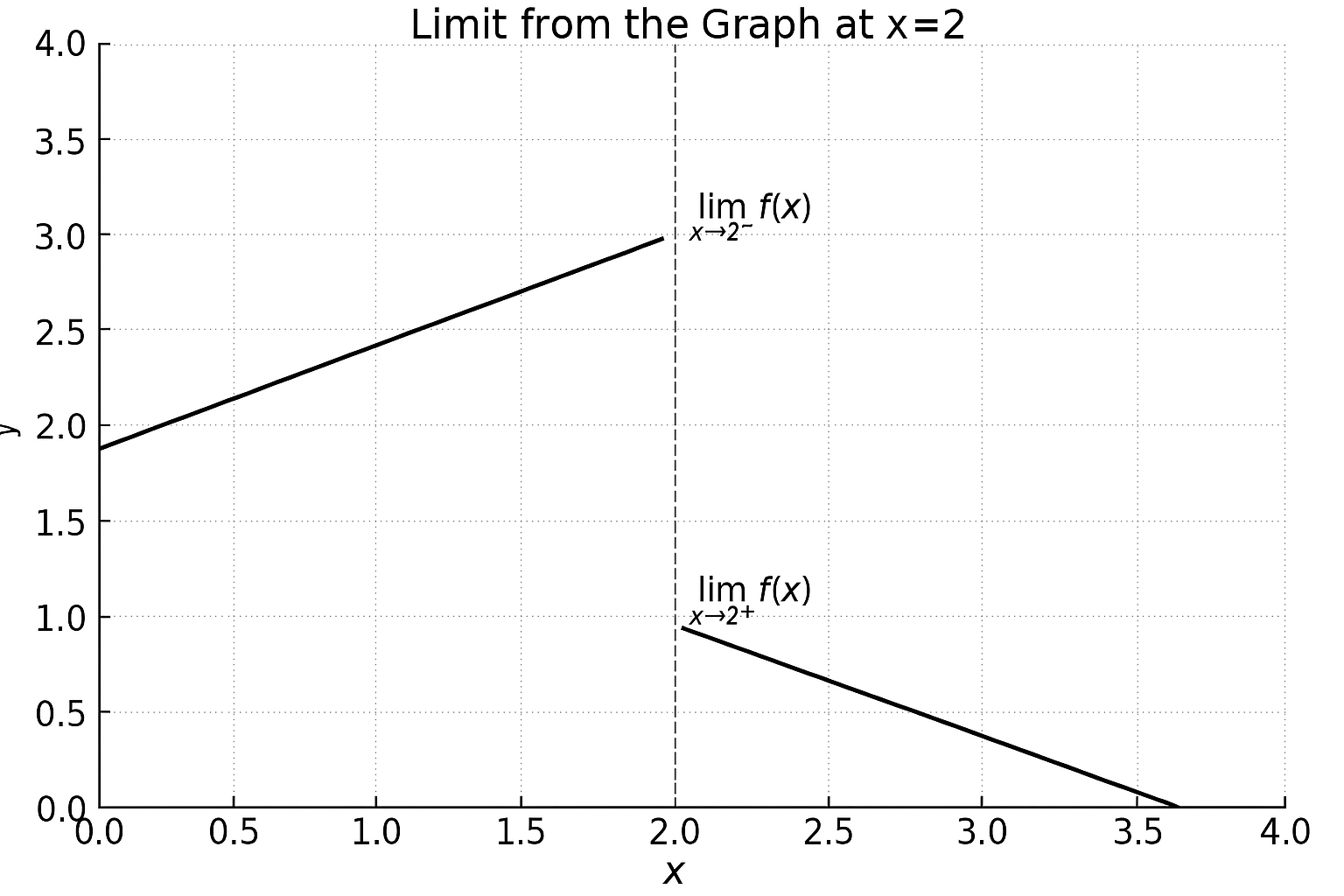
\[ \lim_{x \to 2^-} f(x) = 3 \]
\[ \lim_{x \to 2^+} f(x) = 1 \]
Left and right-hand limits are not equal → limit DNE.
Question 5: Find the limit by factoring.
\[ \lim_{x \to 5} \frac{x^2 - 25}{x - 5} = 10 \]
\[ \lim_{x \to 5} \frac{(x-5)(x+5)}{x-5} = \lim_{x \to 5} (x+5) = 10 \]
Question 6: Find the limit at infinity. What is the horizontal asymptote?
\[ \lim_{x \to \infty} \frac{5x + 3}{x^2 + 2x} = 0 \]
Degree numerator < degree denominator → horizontal asymptote y = 0
Question 7: Find the one-sided limit.
\[ \lim_{x \to 5^+} \frac{x+5}{x-5} = +\infty \]
As \(x \to 5^+\), numerator → 10, denominator → 0^+ → limit = +∞
Question 8: Find the limit of the trigonometric function.
\[ \lim_{x \to 0} \frac{1 - \cos(5x)}{x^2} = \frac{25}{2} \]
Using double-angle identity: \[ \lim_{x \to 0} \frac{1 - \cos(5x)}{x^2} = \frac{25}{2} \]
Question 9: Find the limit at infinity. Does horizontal asymptote exist?
\[ \lim_{x \to -\infty} \frac{x^4 - 2x}{x^2 + 1} = +\infty \]
Degree numerator > degree denominator → limit = +∞ → no horizontal asymptote
Question 10: Find the limit.
\[ \lim_{x \to 2} (x^2 + 5x - 6) = 8 \]
Direct substitution: \(2^2 + 5(2) - 6 = 8\)